Workshop 5: Binary Tree, Binary Search Tree and Algorithms
Table of contents
Part A: Binary Tree Algorithms
Question 1: Binary Tree Traversal
There are three common orders in which the nodes in a binary tree can be traversed. For each of the following binary trees, show the resulting order in which the nodes in the binary tree are visited using:
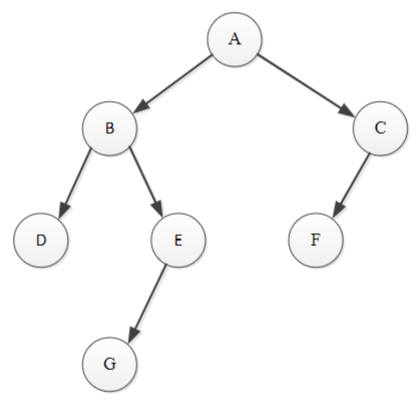
a. Pre-order traversal
Answer: A, B, D, E, G, C, F
In pre-order traversal, the nodes are visited in the following order:
- Visit the root
- Traverse the left subtree
- Traverse the right subtree
This is useful for creating a copy of the tree.
b. Post-order traversal
Answer: D, G, E, B, F, C, A
In post-order traversal, the nodes are visited in the following order:
- Traverse the left subtree
- Traverse the right subtree
- Visit the root
This is useful for deleting the tree, as the leaves are deleted first.
c. In-order traversal
Answer: D, B, G, E, A, F, C
In in-order traversal, the nodes are visited in the following order:
- Traverse the left subtree
- Visit the root
- Traverse the right subtree
This is useful for printing the nodes in a sorted order (in a binary search tree).
Question 2: Binary Search Tree
Which of the following are binary search trees?
a.
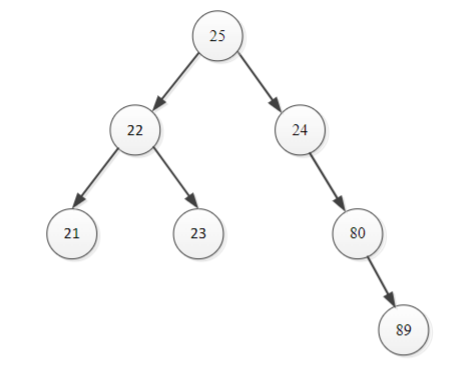
Answer: Not a Binary Search Tree
This is because the right child (24) of the root node (25) is less than the root node.
b.
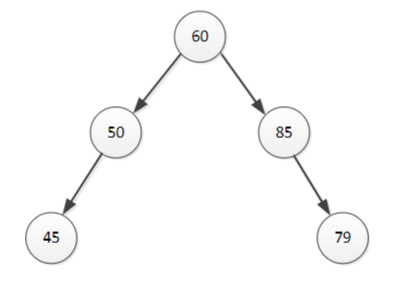
Answer: Not a Binary Search Tree
Looking at the right sub tree, the node (85) has a right child (79) less than itself, which is a same issue as the previous example.
c.
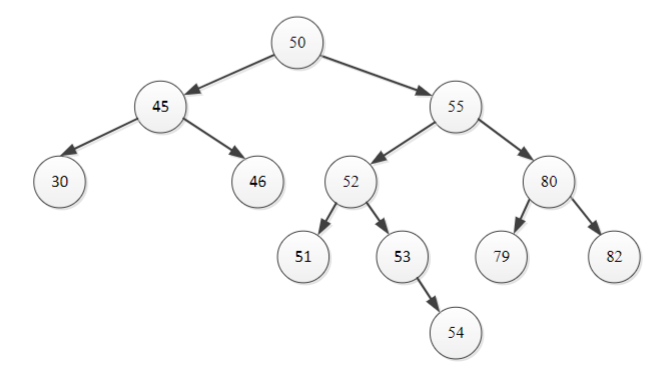
Answer: Binary Search Tree
All left children are less than the parent node, and all right children are greater than the parent node.
Question 3: Search/Deleting/Adding Nodes to a Binary Search Tree
You can try out these using the BST visualisation in this week’s tutorial slides.
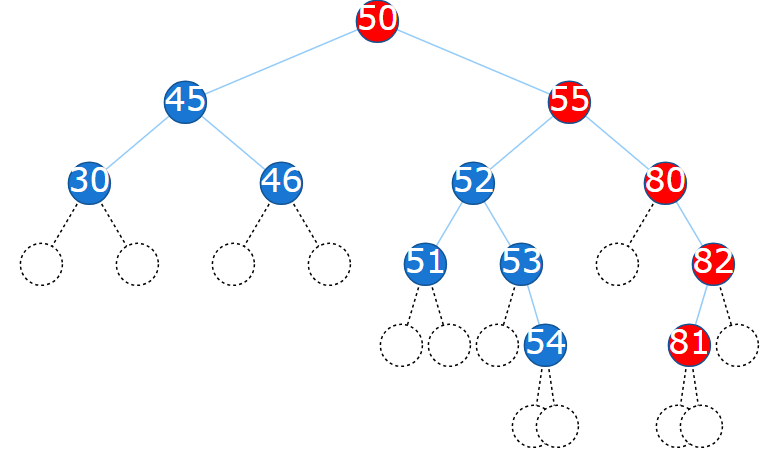
For the valid binary search tree from Question 2:
a) Show the nodes which are visited when searching for:
i. 52
ii. 46
iii. 75
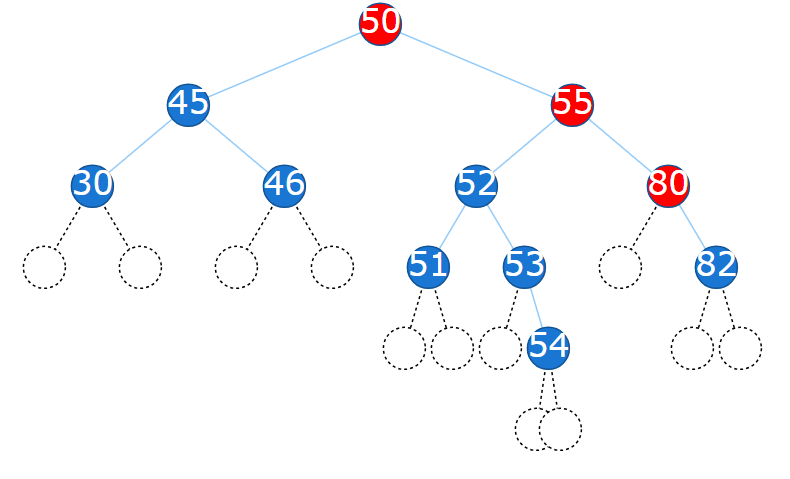
Answer: i. 50, 55, 52 ii. 50, 45, 46 iii. 50, 55, 80, 79
When searching, the algorithm compares the value to the current node.
- If the value is less than the current node, it moves to the left child.
- If the value is greater than the current node, it moves to the right child.
b) Delete the following nodes and show the new binary search tree:
i. 79
ii. 53
iii. 55
Answer
i. 79. Not exist, so no change. Red nodes are the nodes visited.
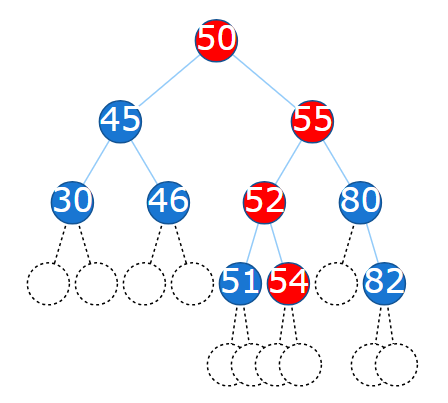
ii. 53. Has a single child, so it is replaced by its child.
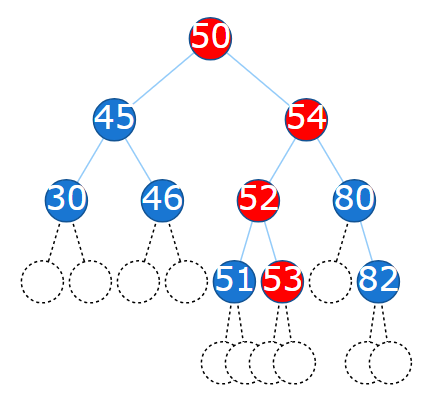
iii. 55. Has two children, so it is replaced by the largest node in its left subtree (54).
c) Add the following nodes and show the new binary search tree:
i. 35
ii. 81
Answer
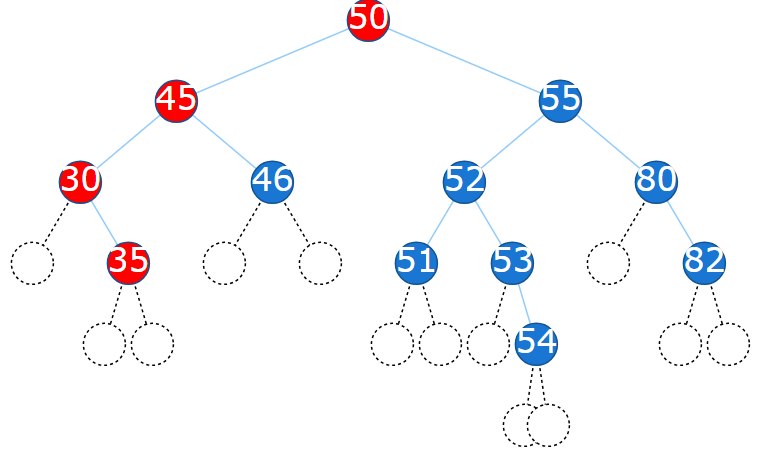
i. 35. Searching for 35 ends at 30, so 35 is added as the right child of 30.
ii. 81. Searching for 81 ends at 82, so 81 is added as the left child of 82.
Part B: Programming Tasks
- You are provided a C# implementation of Binary Search Tree where each node represents a char. Reuse the code to create a Binary Search Tree of Customer objects and test the methods in the Binary Search Tree, including Insert , Delete, Search , PreOrderTravrse , InOrderTraverse and PostOrderTraverse.
Answer: You may copy the following code into your program.
BSTree.cs has the code for the Binary Search Tree implementation (including a BTreeNode class and a BSTree class).
using System;
namespace BinarySearchTree;
public class BTreeNode
{
public IComparable Data { get; set; }
public BTreeNode Left { get; set; }
public BTreeNode Right { get; set; }
public BTreeNode(IComparable item)
{
Data = item;
Left = null;
Right = null;
}
}
public class BSTree
{
private BTreeNode root;
public BSTree()
{
root = null;
}
public bool IsEmpty()
{
return root == null;
}
public bool Search(IComparable item)
{
return Search(item, root);
}
private bool Search(IComparable item, BTreeNode r)
{
if(r != null)
{
if(item.CompareTo(r.Item) == 0)
return true;
else
if(item.CompareTo(r.Item) < 0 )
return Search(item, r.LChild);
else
return Search(item, r.RChild);
}
else
return false;
}
public void Insert(IComparable item)
{
if(root == null)
root = new BTreeNode(item);
else
Insert(item, root);
}
// pre: ptr != null
// post: item is inserted to the binary search tree rooted at ptr
private void Insert (IComparable item, BTreeNode ptr)
{
if (item.CompareTo(ptr.Item) < 0)
{
if (ptr.LChild == null)
ptr.LChild = new BTreeNode(item);
else
Insert(item, ptr.LChild);
}
else
{
if (ptr.RChild == null)
ptr.RChild = new BTreeNode(item);
else
Insert(item, ptr.RChild);
}
}
// there are three cases to consider:
// 1. the node to be deleted is a leaf
// 2. the node to be deleted has only one child
// 3. the node to be deleted has both left and right children
public void Delete(IComparable item)
{
// search for item and its parent
BTreeNode ptr = root; // search reference
BTreeNode parent = null; // parent of ptr
while((ptr!=null)&&(item.CompareTo(ptr.Item)!=0))
{
parent = ptr;
if(item.CompareTo(ptr.Item) < 0) // move to the left child of ptr
ptr = ptr.LChild;
else
ptr = ptr.RChild;
}
if(ptr != null) // if the search was successful
{
// case 3: item has two children
if((ptr.LChild != null)&&(ptr.RChild != null))
{
// find the right-most node in left subtree of ptr
if(ptr.LChild.RChild == null) // a special case: the right subtree of ptr.LChild is empty
{
ptr.Item = ptr.LChild.Item;
ptr.LChild = ptr.LChild.LChild;
}
else
{
BTreeNode p = ptr.LChild;
BTreeNode pp = ptr; // parent of p
while(p.RChild != null)
{
pp = p;
p = p.RChild;
}
// copy the item at p to ptr
ptr.Item = p.Item;
pp.RChild = p.LChild;
}
}
else // cases 1 & 2: item has no or only one child
{
BTreeNode c;
if(ptr.LChild != null)
c = ptr.LChild;
else
c = ptr.RChild;
// remove node ptr
if(ptr == root) //need to change root
root = c;
else
{
if(ptr == parent.LChild)
parent.LChild = c;
else
parent.RChild = c;
}
}
}
}
public void PreOrderTraverse()
{
Console.Write("PreOrder: ");
PreOrderTraverse(root);
Console.WriteLine();
}
private void PreOrderTraverse(BTreeNode root)
{
if(root != null)
{
Console.Write(root.Item);
PreOrderTraverse(root.LChild);
PreOrderTraverse(root.RChild);
}
}
public void InOrderTraverse()
{
Console.Write("InOrder: ");
InOrderTraverse(root);
Console.WriteLine();
}
private void InOrderTraverse(BTreeNode root)
{
if(root != null)
{
InOrderTraverse(root.LChild);
Console.Write(root.Item);
InOrderTraverse(root.RChild);
}
}
public void PostOrderTraverse()
{
Console.Write("PostOrder: ");
PostOrderTraverse(root);
Console.WriteLine();
}
private void PostOrderTraverse(BTreeNode root)
{
if(root != null)
{
PostOrderTraverse(root.LChild);
PostOrderTraverse(root.RChild);
Console.Write(root.Item);
}
}
public void Clear()
{
root = null;
}
}
Customer.cs has the code for the Customer class.
using System;
using System.Collections.Generic;
using System.Text;
namespace BinarySearchTree;
class Customer: IComparable
{
public string FirstName { get; private set; }
public string LastName { get; private set; }
public int Mobile { get; private set; }
public Customer(string lastName, string firstName, int mobileNumber)
{
FirstName = firstName;
LastName = lastName;
Mobile = mobileNumber;
}
public int CompareTo(Object obj)
{
Customer another = (Customer)obj;
if (LastName.CompareTo(another.LastName) < 0)
return -1;
else
if (LastName.CompareTo(another.LastName) == 0)
return FirstName.CompareTo(another.FirstName);
else
return 1;
}
public override string ToString()
{
return (FirstName + " " + LastName + " " + Mobile.ToString() + "\n");
}
}
Program.cs has the code to test the BSTree class with Customer objects.
using System;
using BSTreeInterface;
using BSTreeClass;
namespace BinarySearchTree;
public class Program
{
static public void Main()
{
// build a Binary Search Tree (BST)
//Initially it is empty
IBSTree aBSTree = new BSTree();
// use the Insert method to insert some Customer objects into the BST
aBSTree.Insert(new Customer("Morris", "Scott", 11111111));
aBSTree.Insert(new Customer("Turnbull", "Malcolm", 22222222));
aBSTree.Insert(new Customer("Rudd", "Kevin", 33333333));
aBSTree.Insert(new Customer("Gillard", "Julia", 44444444));
aBSTree.Insert(new Customer("Howard", "John", 55555555));
aBSTree.Insert(new Customer("Bill", "Clinton", 66666666));
aBSTree.Insert(new Customer("Barack", "Obama", 77777777));
// pre-order traversal
aBSTree.PreOrderTraverse();
// in-order traversal
aBSTree.InOrderTraverse();
// post-order traversal
aBSTree.PostOrderTraverse();
// delete a leaf node
aBSTree.Delete(new Customer("Howard", "John", 55555555));
// pre-order traversal
aBSTree.PreOrderTraverse();
// in-order traversal
aBSTree.InOrderTraverse();
// post-order traversal
aBSTree.PostOrderTraverse();
// insert the deleted node back to the BST
aBSTree.Insert(new Customer("Howard", "John", 55555555));
// delete a node that has only one child
aBSTree.Delete(new Customer("Turnbull", "Malcolm", 22222222));
// pre-order traversal
aBSTree.PreOrderTraverse();
// in-order traversal
aBSTree.InOrderTraverse();
// post-order traversal
aBSTree.PostOrderTraverse();
// insert the deleted node back to the BST
aBSTree.Insert(new Customer("Turnbull", "Malcolm", 22222222));
// delete a node that has only one child
aBSTree.Delete(new Customer("Gillard", "Julia", 44444444));
// pre-order traversal
aBSTree.PreOrderTraverse();
// in-order traversal
aBSTree.InOrderTraverse();
// post-order traversal
aBSTree.PostOrderTraverse();
aBSTree.Insert(new Customer("Gillard", "Julia", 44444444));
Customer aCustomer = new Customer("Gillard", "Julia", 44444444);
bool aBool = aBSTree.Search(aCustomer);
if (aBool)
Console.WriteLine(aCustomer.ToString() + "is in the BST");
else
Console.WriteLine(aCustomer.ToString() + "is not in the BST");
// clear the binary tree
aBSTree.Clear();
// pre-order traversal
aBSTree.PreOrderTraverse();
// in-order traversal
aBSTree.InOrderTraverse();
// post-order traversal
aBSTree.PostOrderTraverse();
}
}