Workshop 9: Graph Algorithms – II
Question 1: Adjacency Matrix Revision
To aid in the implementation of Questions 2 & 3 (Dijkstra’s algorithm and Floyd’s algorithm) create an adjacency matrix for the following weighted directed graph.
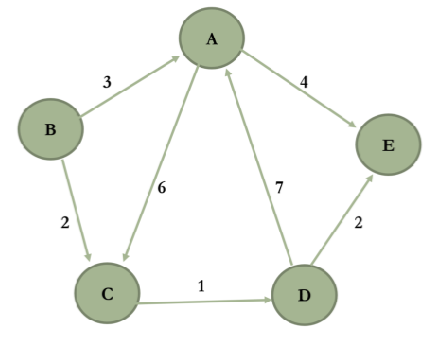
As a revision from previous workshop for the interested students also construct an Adjacency List for the graph.
Answer
The adjacency matrix for the graph is as follows:
A B C D E A ∞ ∞ 6 ∞ 4 B 3 ∞ 2 ∞ ∞ C ∞ ∞ ∞ 1 ∞ D 7 ∞ ∞ ∞ 2 E ∞ ∞ ∞ ∞ ∞ And the adjacency list for the graph is as follows:
Vertex Adjacent Vertices (Weight) A C(6), E(4) B A(3), C(2) C D(1) D A(7), E(2) E
Question 2: Dijkstra’s Algorithm
Use Dijkstra’s algorithm to find the shortest paths and distances to all vertices, with A as the source using the following graph. Show full details of your working to illustrate your understanding of the algorithm.
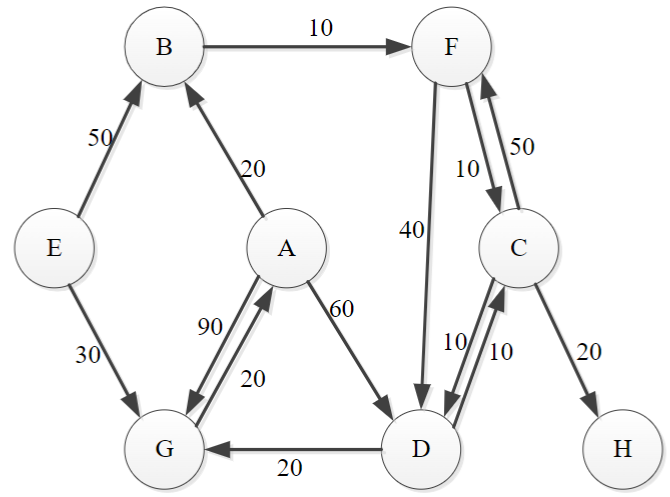
Answer
The adjacency matrix for the graph is as follows:
A B C D E F G H A ∞ 20 ∞ 60 ∞ ∞ 90 ∞ B ∞ ∞ ∞ ∞ ∞ 10 ∞ ∞ C ∞ ∞ ∞ 10 ∞ 50 ∞ 20 D ∞ ∞ 10 ∞ ∞ ∞ 20 ∞ E ∞ 50 ∞ ∞ ∞ ∞ 30 ∞ F ∞ ∞ 10 40 ∞ ∞ ∞ ∞ G 20 ∞ ∞ ∞ ∞ ∞ ∞ ∞ H ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ The table below shows the list of vertices visited in each iteration of the Dijkstra’s algorithm. In each iteration:
- Via the most recently visited vertex, calculate the distance to each unvisited vertex, and update if new distance is shorter.
- Find the closest unvisited vertex and mark it as visited.
Iteration Visited Vertices A B C D E F G H Closest Unvisited Node Notes 0 [A] ∞ 20 ∞ 60 ∞ ∞ 90 ∞ B (20) Initial state (same as source row) 1 [A, B] ∞ 20 ∞ 60 ∞ 30 90 ∞ F (30) B goes to F 2 [A, B, F] ∞ 20 40 60 ∞ 30 90 ∞ C (40) F goes to C (30 + 10 = 40 < ∞), D (30 + 40 = 70 > 60) 3 [A, B, F, C] ∞ 20 40 50 ∞ 30 90 60 D (50) C goes to D (40 + 10 = 50 < 60), H (40 + 20 = 60); F has already been visited 4 [A, B, F, C, D] ∞ 20 40 50 ∞ 30 70 60 G (70) D goes to G (50 + 20 = 70 < ∞); C has already been visited 5 [A, B, F, C, D, G] ∞ 20 40 50 ∞ 30 70 60 H (70) G does not go to any unvisited nodes 6 [A, B, F, C, D, G, H] ∞ 20 40 50 ∞ 30 70 60 E (∞) H does not go to any unvisited nodes To find the shortest path, find the iteration where the distance to the destination node is last updated from ∞.
- B was last updated in iteration 0, so the shortest path from A to B is A → B.
- C was last updated in iteration 2, so the shortest path from A to C is A → B → F → C.
- D was last updated in iteration 3, so the shortest path from A to D is A → B → F → C → D.
- E was never updated from ∞, so there is no path from A to E.
- F was last updated in iteration 1, so the shortest path from A to F is A → B → F.
- G was last updated in iteration 4, so the shortest path from A to G is A → B → F → C → D → G.
- H was last updated in iteration 3, so the shortest path from A to H is A → B → F → C → H.
Question 3: Floyd’s Algorithm
Use Floyd’s algorithm to find the shortest distance between every pair of vertices in the graph below. Show full details of your working to illustrate your understanding of the algorithm showing how the distance matrix updates as you work through each node. In your working show which matrix elements have been updated from the previous step.
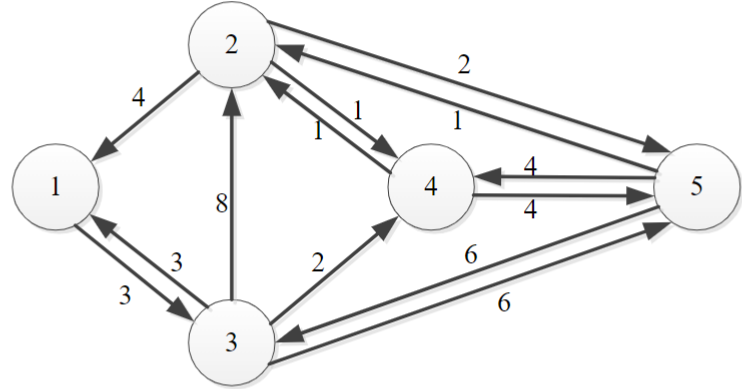
As there are 5 nodes in the graph how many passes over the algorithm will be required?
Edges:
Answer
The adjacency matrix for the graph is as follows:
1 2 3 4 5 1 ∞ ∞ 3 ∞ ∞ 2 4 ∞ ∞ 1 2 3 3 8 ∞ 2 6 4 ∞ 1 ∞ ∞ 4 5 ∞ 1 6 4 ∞ Step 1: Pass through node 1
1 2 3 4 5 1 ∞∞3∞∞2 4∞ 7 1 2 3 38 6 2 6 4 ∞1 ∞ ∞ 4 5 ∞1 6 4 ∞ Tip: Look for rows and columns that are not infinity, and update the intersection of the row and column with the sum of the two values (if it is less than the current value).
Updated values are shown in bold.
Step 2: Pass through node 2
1 2 3 4 5 1 ∞ ∞3 ∞ ∞ 2 4∞7123 3 86 2 6 4 5 18 2 3 5 5 16 2 3 Step 3: Pass through node 3
1 2 3 4 5 1 6 11 35 9 2 4 15 71 2 3 386264 5 1 82 3 5 5 1 62 3 Step 4: Pass through node 4
1 2 3 4 5 1 6 6 3 58 2 4 2 7 12 3 3 3 6 25 4 518235 5 1 6 23 Step 5: Pass through node 5
1 2 3 4 5 1 6 6 3 5 82 4 2 7 1 23 3 3 6 2 54 5 1 8 2 35 51623Number of passes equals the number of nodes in the graph, which is 5, however, the number of comparisons is equal to the number of nodes cubed, which is 125.
Question 4: Implementation of Floyd’s Algorithm
A driver program (Program.cs) has been provided for testing Floyd’s algorithm. A simple graph has been provided as an input into the algorithm which is initialized in Main(). Implement Floyd’s algorithm using the pseudo-code provided below.
If the implementation is correct, the following matrix with the shortest distances between each pair of vertices should be shown as below. (INF means there is no path between the vertices)
Answer
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace FloydsAlgorithm { class Program { // Number of vertices in the graph static int V = 5; /* Define Infinite as a large enough value. This value will be used for vertices not connected to each other */ static int INF = 99999; static void Main(string[] args) { int[,] graph = { {INF, 8, INF, 9, 4}, {INF, INF, 1, INF, INF}, {INF, 2, INF, 3, INF}, {INF, INF, 2, INF, 7}, {INF, INF, 1, INF, INF} }; // Print the solution FloydsAlgorithm(graph); Console.ReadKey(); } // A function to print the solution matrix // void printSolution(int dist[][V]); // Solves the all-pairs shortest path problem using Floyd Warshall algorithm static void FloydsAlgorithm(int[,] graph) { /* dist[][] will be the output matrix that will finally have the shortest distances between every pair of vertices */ int[,] dist = new int[V, V]; int i, j, k; /* Initialize the solution matrix same as input graph matrix. Or we can say the initial values of shortest distances are based on shortest paths considering no intermediate vertex. */ for (i = 0; i < V; i++) for (j = 0; j < V; j++) dist[i, j] = graph[i, j]; /* Add all vertices one by one to the set of intermediate vertices. ---> Before start of a iteration, we have shortest distances between all pairs of vertices such that the shortest distances consider only the vertices in set {0, 1, 2, .. k-1} as intermediate vertices. ----> After the end of a iteration, vertex no. k is added to the set of intermediate vertices and the set becomes {0, 1, 2, .. k} */ for (k = 0; k < V; k++) { // Pick all vertices as source one by one for (i = 0; i < V; i++) { // Pick all vertices as destination for the // above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest path from // i to j, then update the value of dist[i][j] if (dist[i, k] + dist[k, j] < dist[i, j]) dist[i, j] = dist[i, k] + dist[k, j]; } } } // Print the shortest distance matrix printSolution(dist); } /* A utility function to print solution */ static void printSolution(int[,] dist) { Console.Write("Following matrix shows the shortest distances\n" + " between every pair of vertices \n"); Console.Write(" "); for (int m = 0; m < V; m++) { Console.Write(" " + m); } Console.Write("\r\n"); Console.WriteLine("======================================================="); for (int i = 0; i < V; i++) { Console.Write(" " + i); for (int j = 0; j < V; j++) { if (dist[i, j] == INF) { Console.Write(" " + "INF"); } else { Console.Write(" " + dist[i, j]); } } Console.Write("\r\n"); } } } }